GBS 6 Speicherverwaltung 内存管理

Einführung

首先来看一下计算机存储的层次结构：

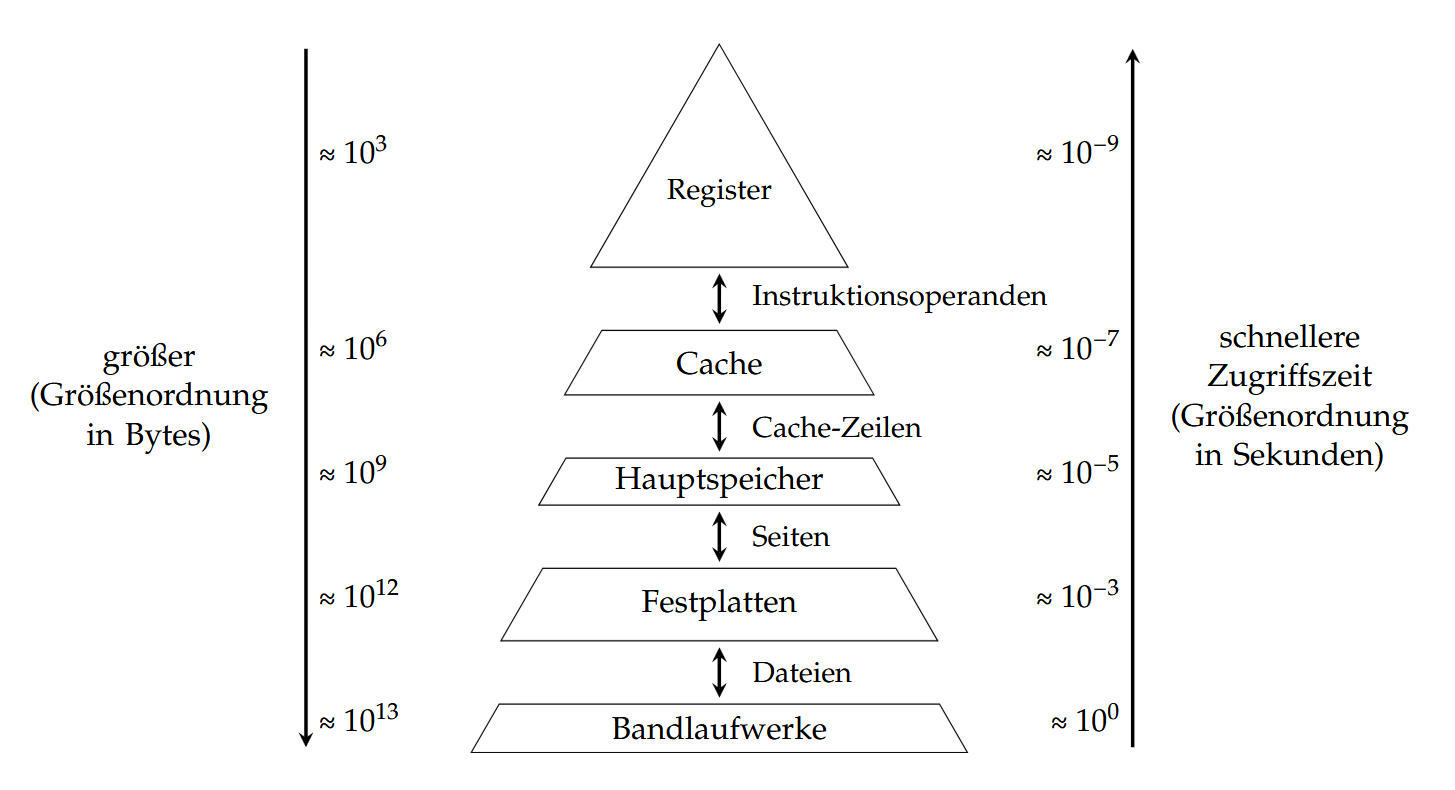
从上往下依次是寄存器、缓存、内存、硬盘以及磁带驱动器。存储空间大小（从上往下）依次递增，但读取速度依次递减。

我们这章主要关注内存（Hauptspeicher）。

物理内存管理

假如所有程序可以完全访问整个物理内存，那么每个程序都有可能占用整个主内存，甚至可能覆盖掉系统内存区域，导致系统崩溃。包括程序直接也可能会相互干扰。所以我们希望给每个进程分配独立的存储空间。

寻址（Adressierung）

而为了更好地管理物理地址空间（Physischer Adressraum），我们会从中抽象出逻辑地址空间（Logischer Adressraum），然后通过内存映射（Speicherabbildung，Memory Address Translation）将逻辑地址转换成实际的物理地址。这种内存映射也叫做寻址（Adressierung）。

寻址方式一般有3种：

直接寻址（Direkte Adressierung）

这种寻址的映射相当于是 $f = id$ 。图示：

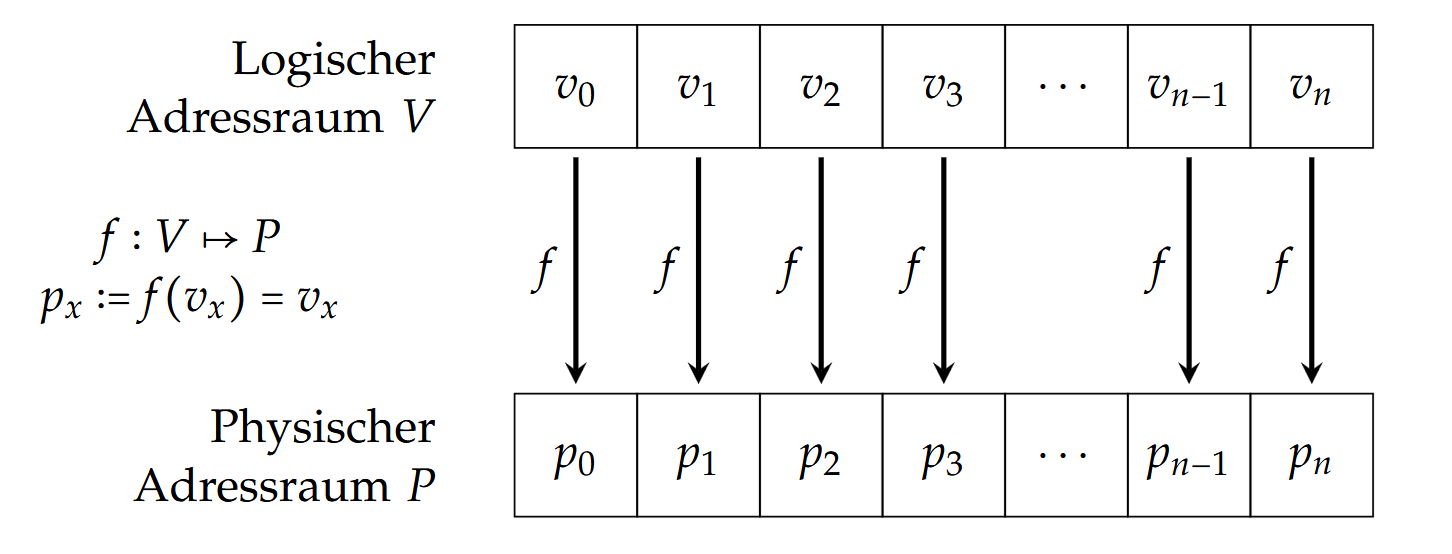
但一旦有多个程序运行的话，我们会碰到以下问题：

大量交换（Extensives Swapping）

在某一时刻一定是只有一个程序在运行并且使用内存空间，所以当操作系统想要切换运行的程序时，需要把当前运行程序的内存内容保存到硬盘，然后从硬盘加载下一个程序到内存中。

这样会导致效率极其低下（或者说非常慢）。
重定位（Relokation）

由于程序可以被加载到内存的不同位置，所以每次重新分配地址时需要改写（重定位）所有的地址，会非常的麻烦。（可以看下面举的例子）

基址寻址（Basis-Adressierung）

每一个进程会得到一个基址（Basisadresse）$b_x$ ，这个进程的所有地址都是基于这个基址的一个相对地址。

图示：

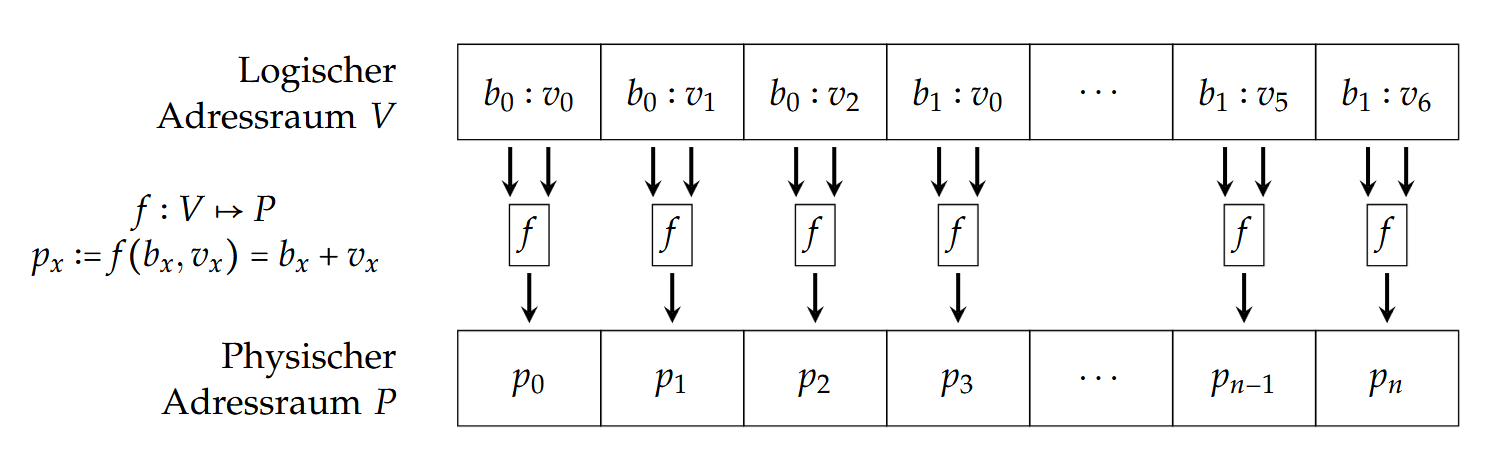
举个例子区分一下基址寻址（Basis-Adressierung）和直接寻址（Direkte Adressierung）：假设我们现在的内存空间有15个Block，并且有2个程序在使用内存，我们将1-5分给第一个程序，把6-10分给第二个程序。如果是直接寻址的话，第一个程序的地址需要记录成（1，2，3，4，5），第二个需要记录（6，7，8，9，10）。但如果是基址寻址的话，第二个只需要记录（5；1，2，3，4，5），主要会记录相对位置。这样一来在重新分配内存空间时只需要修改basis（也就是5）即可（比如说（10；1，2，3，4，5）），其他的不需要改变。

当然基址寻址（Basis-Adressierung）也有个缺点，那就是每次计算地址时都需要进行一次加法操作。（Aufwendige Additionsoperation）

段式寻址（Segmentadressierung）

将Adressraums分成不同长度的逻辑段（logische Segmente），比如说分成Stack-, Daten-, Code-Segment。这样做的好处是可以给每一段内容不同的权限（Zugriffsberechtigungen），以提高安全性，针对pwn的攻击特别有用。

每个段需要两个基本信息：段起始地址（Segmentanfangsadresse）和段的长度（Länge des Segments）。

CPU通常提供一个段寄存器（Segmentregister）来保存段信息。

只不过主要是32 位操作系统会使用段机制，而在64 位系统中基本不用段机制，最多用于线程管理（TLS）和兼容性支持。

我们来看一下x86里的段式寻址（Segmentadressierung）的例子：

x86 架构会使用一个叫做全局描述符表（Global Descriptor Table, GDT）的数据结构来管理段，每一项会包含以下信息：

基地址（Basisadresse）
段的长度（Länge des Segments）
标志位（Flags）：例如Zugriff以及Segment的类型（Code，Daten还是Stack）

而段寄存器（Segmentregister）中保存的不是地址，而是GDT表中的一个索引。

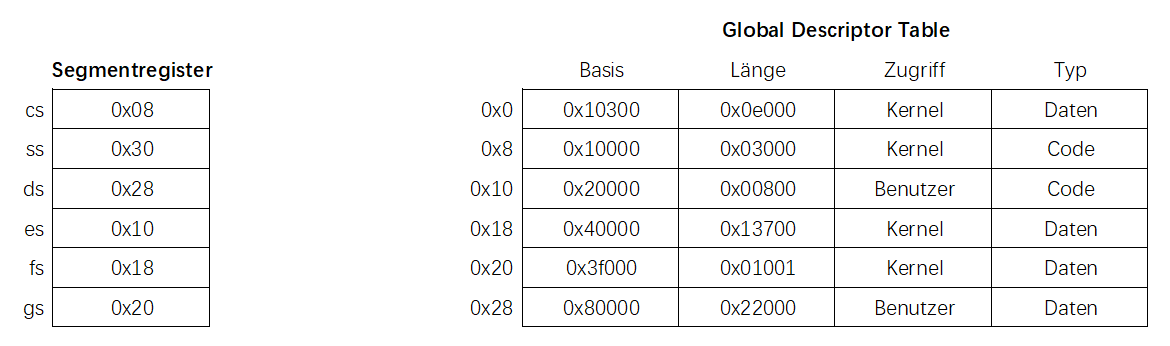
1. 想要访问 cs:0x800 的话，需要先在段寄存器（Segmentregister）找到cs对应的值，也就是 0x08，然后找到这个值在DGT对应的那一行信息。随后计算 0x10000 + 0x800 = 0x10800。确认它在范围内，所以这个就是我们要的地址。

2. 想要访问 es:0x800 的话，需要先在段寄存器（Segmentregister）找到es对应的值，也就是 0x10，然后找到这个值在DGT对应的那一行信息。随后计算 0x20000 + 0x800，会发现超出范围了，因为它的长度只有 0x00800，所以会返回 “Segmentation Fault”。

空闲内存管理（Freispeicherverwaltung）

存储结构

位图（Bitmap）

将存储空间分成相同大小的块（Blöcke），每个块用一个bit标记，1表示已占用，0表示空闲。这一串内容就是位图（Bitmap）。

例子：

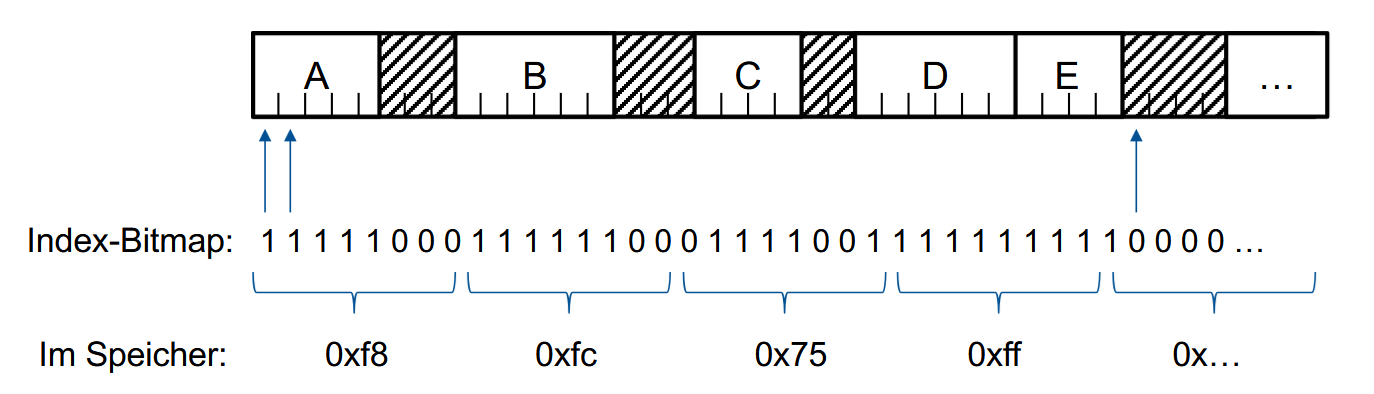
但是实现过程中会遇到一个问题：Blcok的大小该怎么选择呢？选小了就会需要更大位图，但选大了又容易导致浪费。

优势：

可以简单快速地访问固定大小的内存块。

缺点：

假如有个进程需要k个Block，那么就需要在位图里找到7个连续的0，这个的开销就太大了。

链表（Verkettete Liste）

还是将存储空间分成相同大小的块（Blöcke），然后链表记录块的占用信息：

链表的每一项存储：

开始地址
长度
指向下一项的指针（einen Zeiger auf den nächsten Eintrag (oder Terminator T == NULL)）

例子：

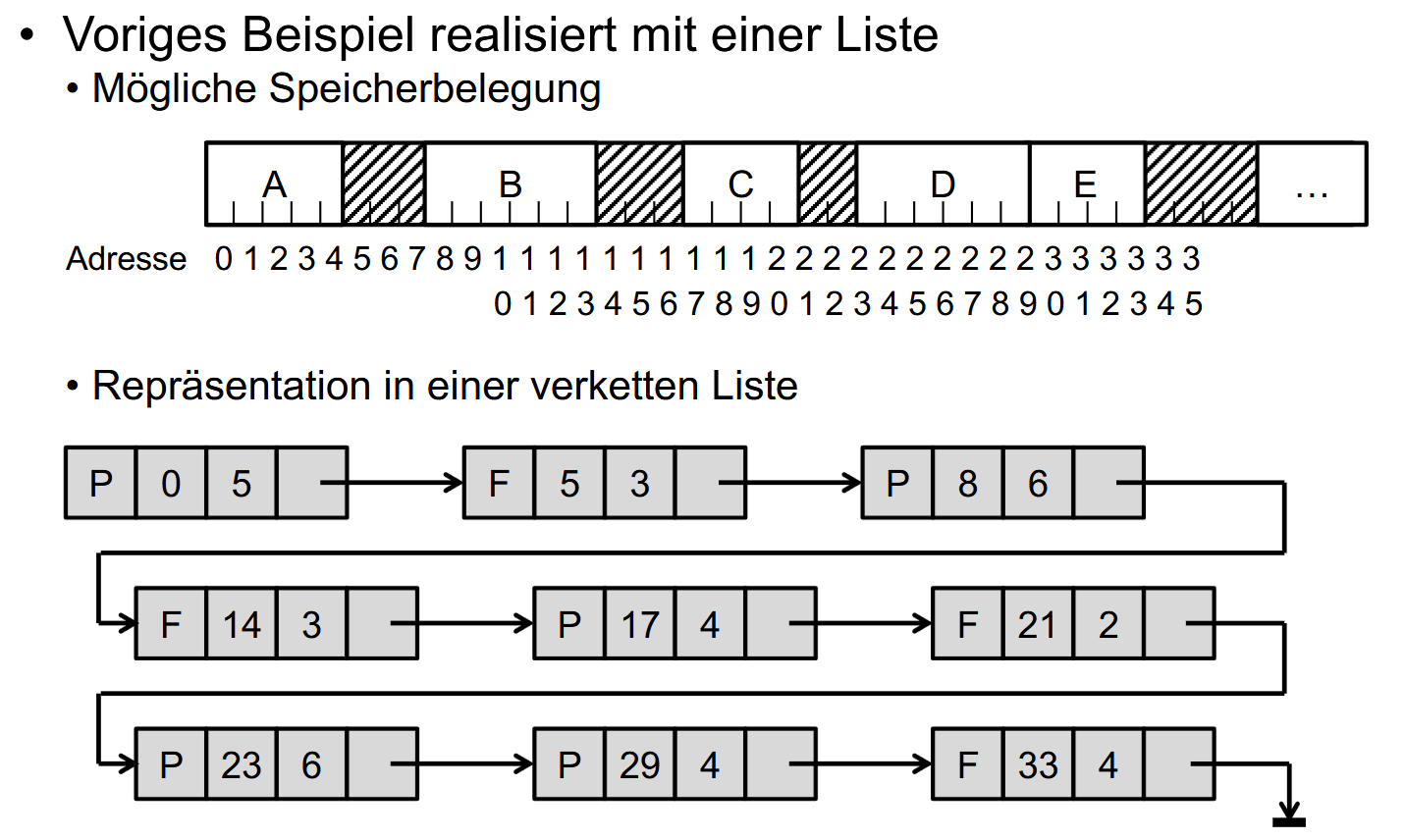
P表示已被进程占用，F表空闲。

优点：

灵活（Flexible Speicheraufteilung）

缺点：

需要线性搜索（Lineare Suche）

需要挨个找有没有合适的。
没有固定的管理结构

优化的办法：

分别维护两个链表，一个存储已分配的内存块，一个存储空闲的内存块。
按照内存块大小排序
使用平衡树结构管理链表（(balancierter) Baumstruktur）
同时使用多个链表

内存分配策略（Belegungstrategien）

由于需要一直分配再释放进程的存储空间，所以存储空间容易碎片化。比如说在上面那张图里有着好几个空闲的连续的存储空间，我们该如何给每个进程选择一块合适的位置呢？

一般会用到以下几个策略：

（以这个为例:）

First-Fit

从前往后，找到大小够的直接给。

Next-Fit

从上次停止的地方开始，找到够的直接给。

Best-Fit

分配“最小剩余空间”的空闲块（Freibereich mit dem geringsten Verschnitt）

Worst-Fit

分配“最大剩余空间”的空闲块（Freibereich mit dem größten Verschnitt）

Buddy-Algorithmus

将存储空间分成 $2^k$ 大小的Block，where $l \leq k \leq u$，$2^l$是最小的可占用的空间大小，$2^u$是最大的可占用的空间大小。当一个进程需要的存储空间为 $x$ 时，会给它分配一块大小为 $2^{\lfloor log_2(x) \rfloor}$ 的Block。

这样一来每次最多会浪费半个Block大小的存储空间。

分配的具体算法看这个例子就好：（需要额外注意它合并空闲块的算法）

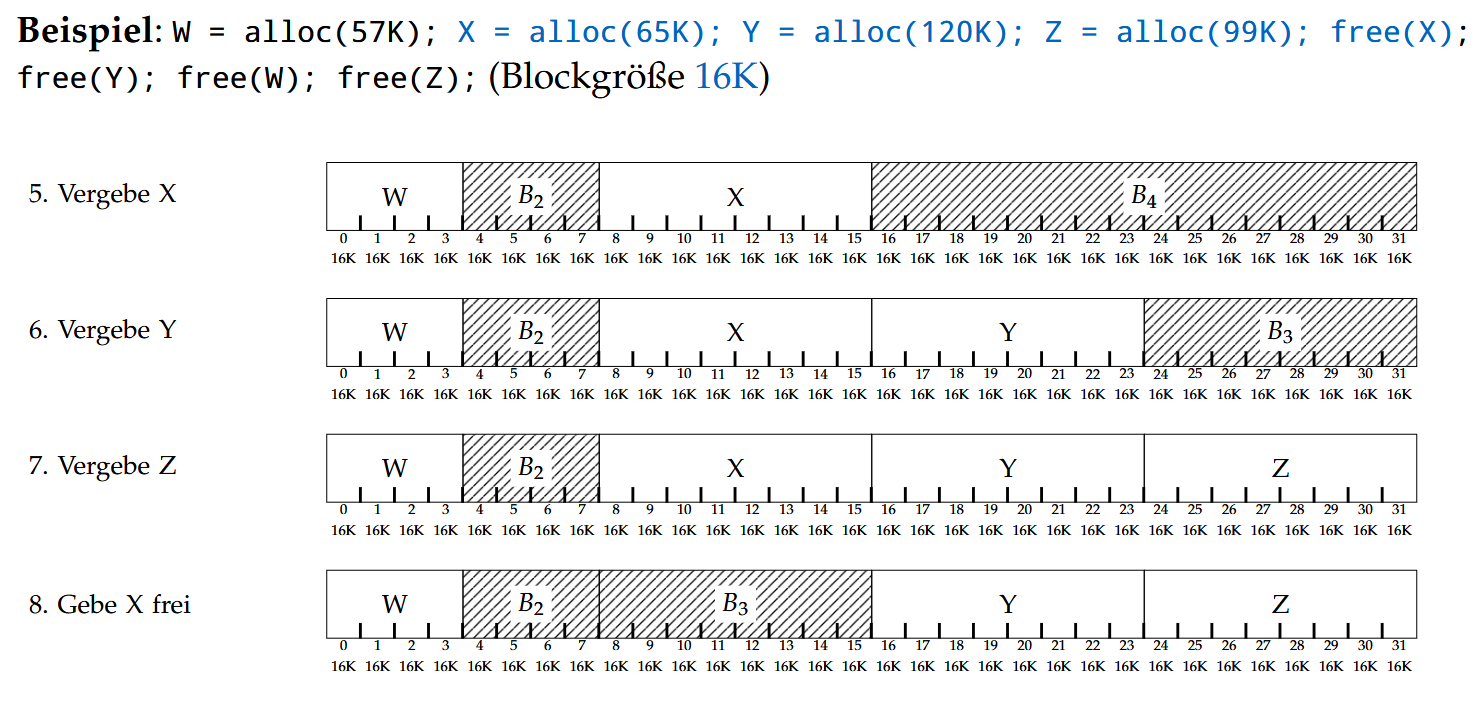
碎片化（Fragmentierung）

一般会分成内部碎片与外部碎片。

内部碎片（Interne Fragmentierung）：在按块分配内存时，通常会分配多于实际所需的内存。这部分多余的内存区域既不能被当前进程使用（内部），也不能被其他进程使用（外部）。也就是会产生很多碎片（Verschnitt）。这些多余的部分就被叫做内部碎片。

例如Buddy-Algorithmus主要带来的便是内部碎片。它给每个进程分配了一个Block之后，这个Block里多余的部分是不会分配给其他进程的。

外部碎片（Externe Fragmentierung）：由于创建和释放内存块的动态变化，会在主存中产生空洞（Löcher）。即使总的空闲内存量是足够的，也可能没有一个足够大的连续内存区域来满足一个请求。这些空闲内存就被叫做外部碎片。

比如说使用Best-Fit策略，就会剩下来很多小的不连续的空闲块。

虚拟内存管理（Virtuelle Speicherverwaltung）

一般情况下，进程的虚拟地址空间是大于实际可用的物理内存的。所以我们同样需要管理虚拟内存，以决定将哪些部分加载到（物理的实际）内存中。

最常用的实现方式便是分页（Paging）：

将虚拟地址空间被划分为页面（Seiten，Pages），内存（Hauptspeicher）被划分为物理页框（Kacheln，Frames）。通常每一页和每个页框的大小相同，或者至少页的大小是页框大小的倍数。

操作系统需要做的便是将页面映射到页框（Abbilden von Seiten auf Kacheln）。

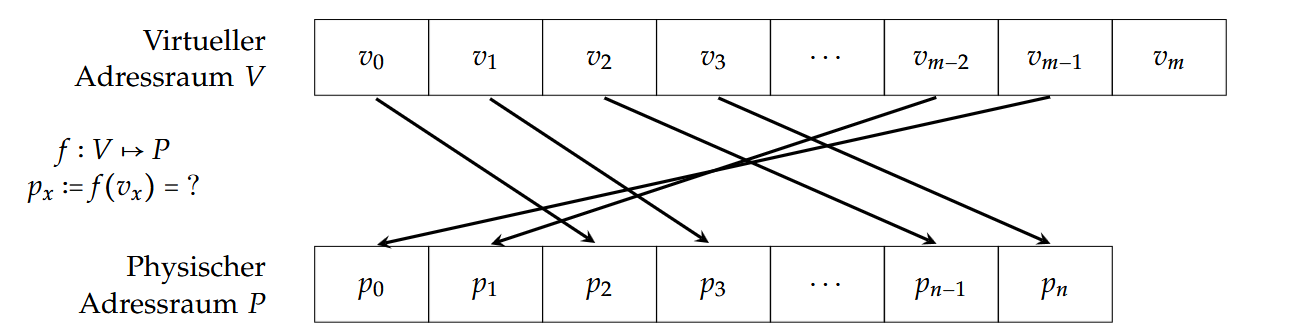
这个映射具体由内存管理单元（Memory Management Unit，MMU）完成。

Paging中三个重要概念：（下面会详细讲）

页表（Page Table）：

负责管理虚拟页与物理页框之间的映射关系，操作系统为每个进程维护一张页表。
缺页异常（Seitenfehler，Page Fault）：

当访问一个尚未被加载到内存的虚拟页时，就会产生一个页错误（Page Fault），硬件会发出一个中断信号。操作系统响应这个中断，把缺失的页从磁盘加载到内存
页面换入（Seiteneinlagerung）：

如果内存已满，则需要将已有的页移出（换出）来腾出空间，被换出的页会被保存到硬盘中。

流程：

程序访问虚拟页 → 检查页表 → 若页不在内存 → 触发页错误（Page Fault） → OS 调入页面 → 若内存满 → 页面置换 → 更新页表 → 继续执行

硬件组件

如之前提到的，内存管理单元（Memory Management Unit，MMU）负责完成地址的映射。

它的工作流程如图：

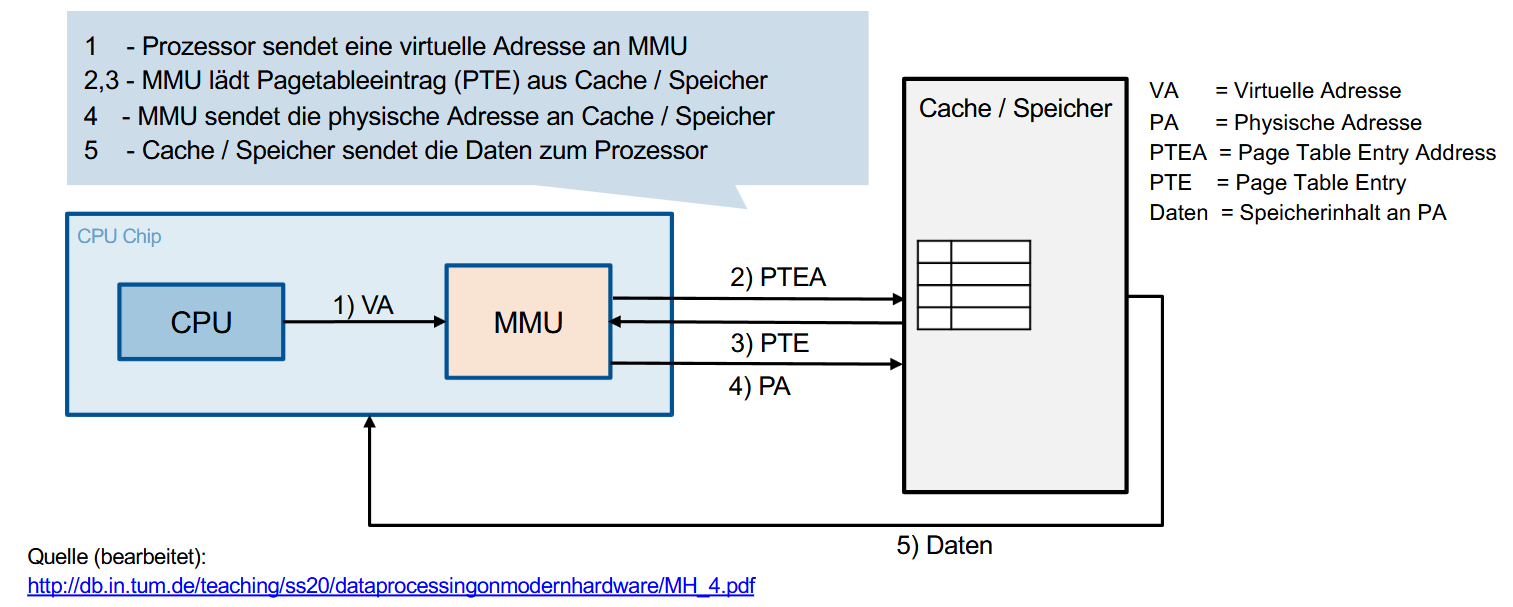
CPU 发送虚拟地址（VA）给 MMU
MMU 根据虚拟地址确定 Page Table Entry 的地址（PTEA）
MMU 从缓存或内存中读取页表项（PTE）
MMU 根据页表项计算出物理地址（PA）
缓存/内存将物理地址对应的数据（Daten）发送回 CPU

但这样会带来一个问题：由于页表通常存放在主存中，所以地址转换（Adressabbildung）的开销会非常大。

因此可以利用缓存（Cache）来改善这个问题：地址转换后备缓冲区（Translation Lookaside Buffer，TLB），它负责存储近期访问过的页表项（Page Table Entry）。

流程：

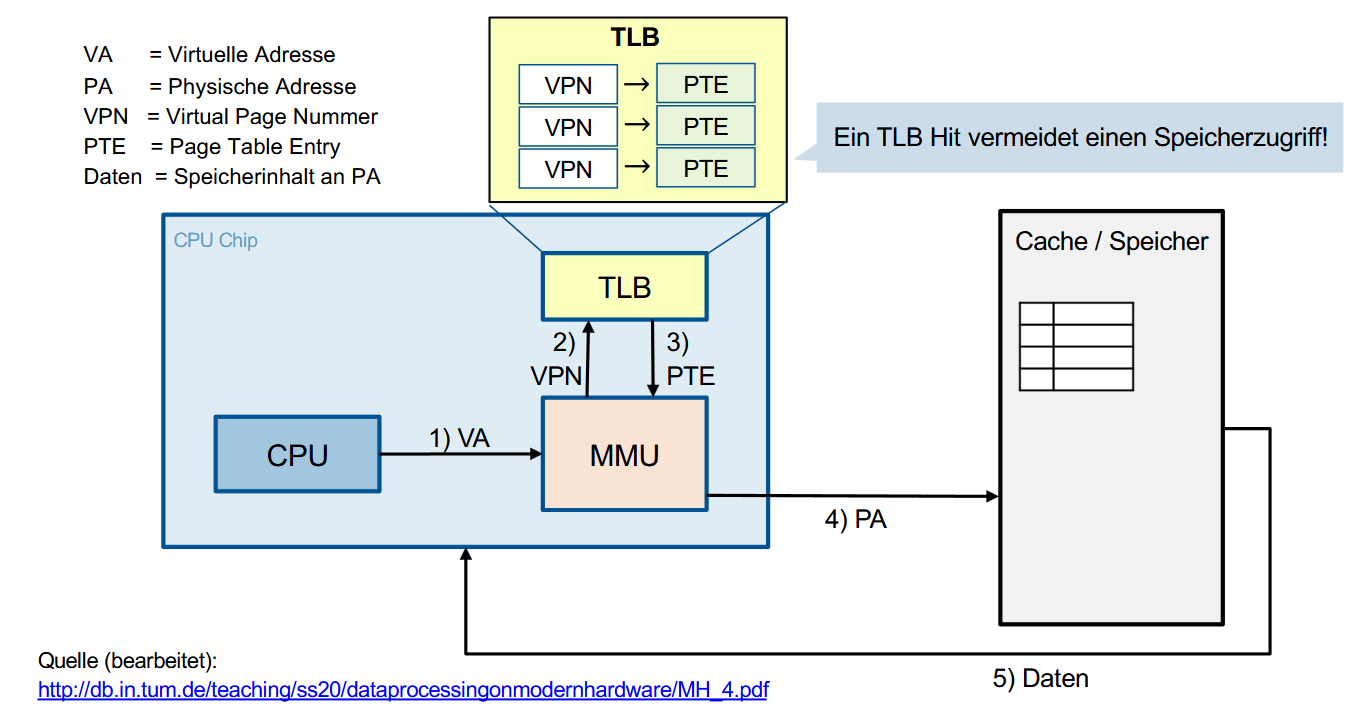
CPU 发送虚拟地址 VA
MMU 提取出虚拟页号 VPN，查询 TLB
如果 TLB 命中（TLB Hit），直接获得页表项（PTE）
MMU 根据 PTE 生成物理地址（PA）
数据从物理内存中返回到 CPU

没有 Hit 的情况叫做 TLB Miss，会需要一次额外的内存访问来加载页表项（PTE）：

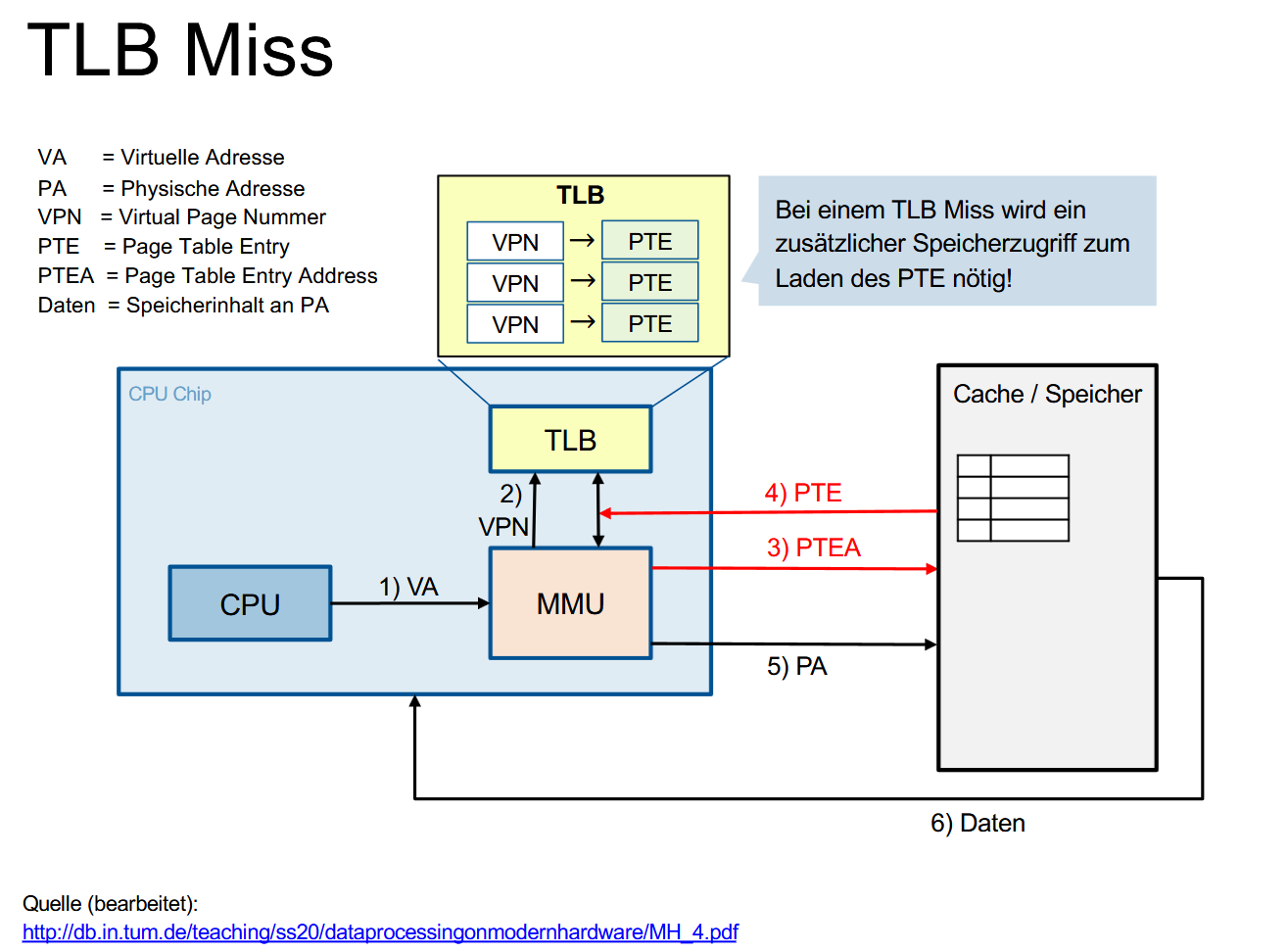
页表（Page Table）

一个虚拟地址 v 会被解释为v=(s,w)，其中s表示页号（Seitenummer），w表示偏移量（Offset）。

每一页都对应一个页表项（1 Page-Table-Eintrag pro Seite），而这个页表项里会存储页框号（Frame-Nummer）。在转换地址时，s会被直接转换成页框号（Frame-Nummer），然后和w拼起来组成真正的物理地址。如图：

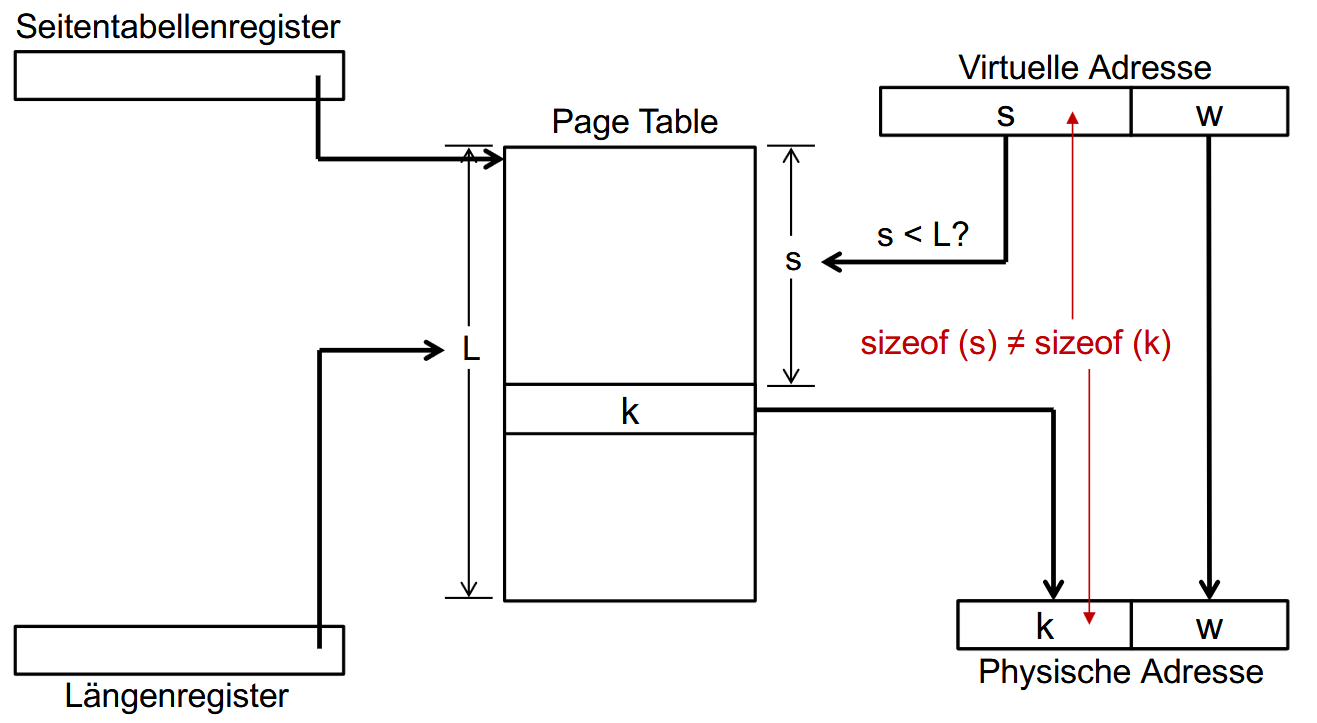
具体的转换过程可以看文章末尾的相关例题。

而页表中除了地址，还会存储附加信息，通过单个位（Bit）来表示：

P（present）位：是否存在

表示对应的物理地址是否存在/有效
U/S（user/supervisor）位：用户/内核模式访问控制

指示是否只有操作系统内核（Betriebssystemkern）可以访问该页面
R（referenced）/ A（accessed）位：是否被访问过

只要这个页面被访问（zugegriffen），CPU就会自动设置这一位（为1）。
M（modify）/ Dirty Bit：是否被修改过

只要这页里有至少一个字节被写入（geschrieben），CPU就会自动设置这一位（为1）。
XD（execute-disable）位：禁止执行位

表示该页是否允许执行指令。属于保护措施。

多级页表（Mehrstufige Seitentabellen）

如果虚拟地址空间很大，那么相应的页表（Page Table）也非常大，意味着将整个页表放入内存会占用大量内存资源。

所以需要引入多级页表结构，每一级页表只负责一部分地址空间，按需加载。

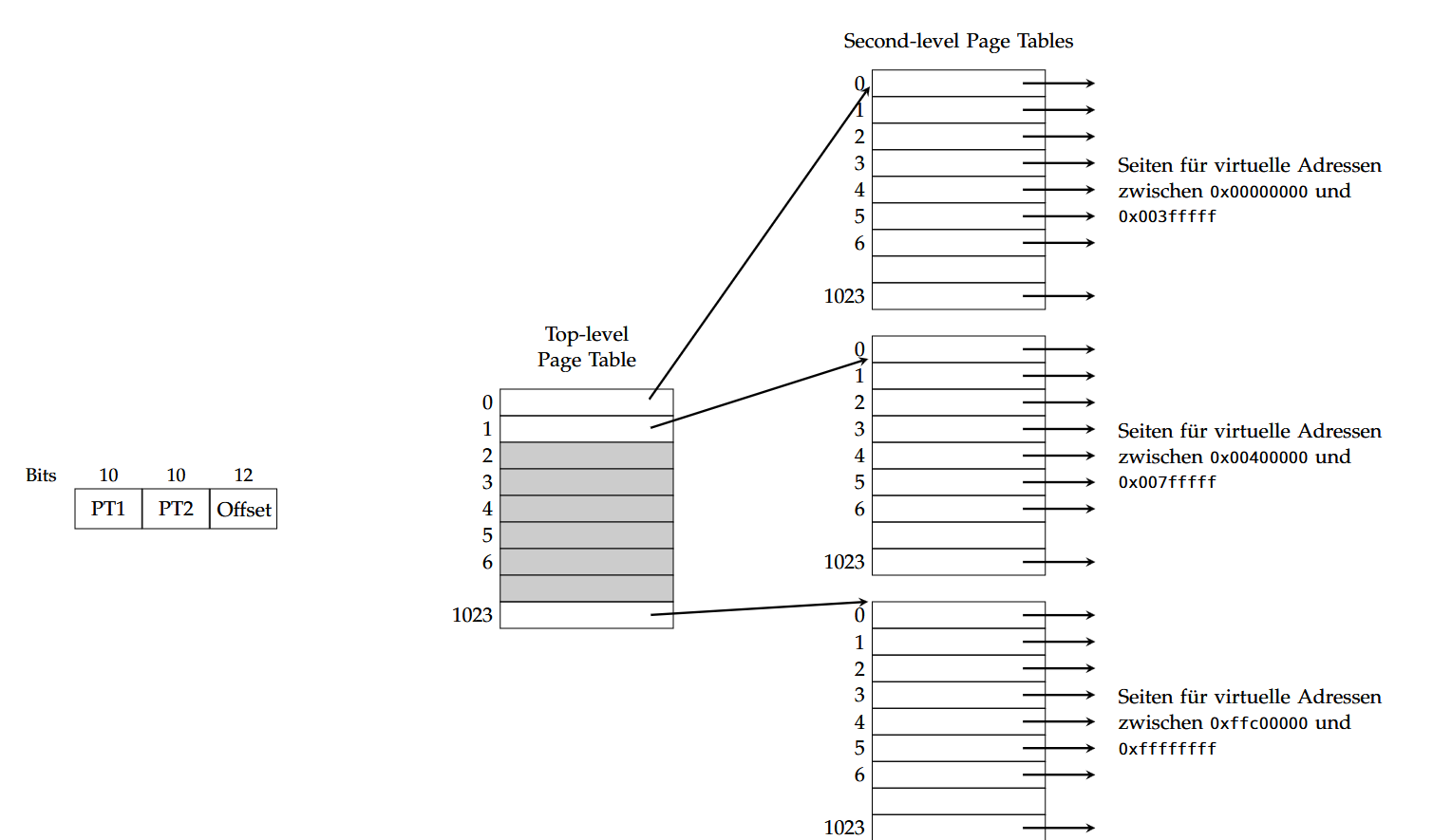
页错误（Seitenfehler，Page Fault）

当程序访问一个虚拟地址时，如果该地址对应的页面不在内存中（即页表中的 P-Bit 未设置），就会发生页错误（Seitenfehler，Page Fault）。硬件会触发中断（Interrupt），交由操作系统处理，执行页错误处理器（Page-Fault-Handler）。

处理时分2种情况：

页面被换出（ausgelagert）：

查找是否有空闲页框（Kachel）：
- 有空闲：直接加载页面
- 无空闲：使用页面置换算法（Seitenersetzungsstrategien）释放空间
页面不存在也未被换出（nicht ausgelagert）

操作系统会触发内存保护错误（Speicherschutz-Fehler）

之后便会更新页表项（Page-Table-Eintrag）：设置P-Bit，清除R-Bit和M-Bit。

这些操作都完成之后便会恢复程序的状态。

目前这些转换地址的流程总结一下就是：

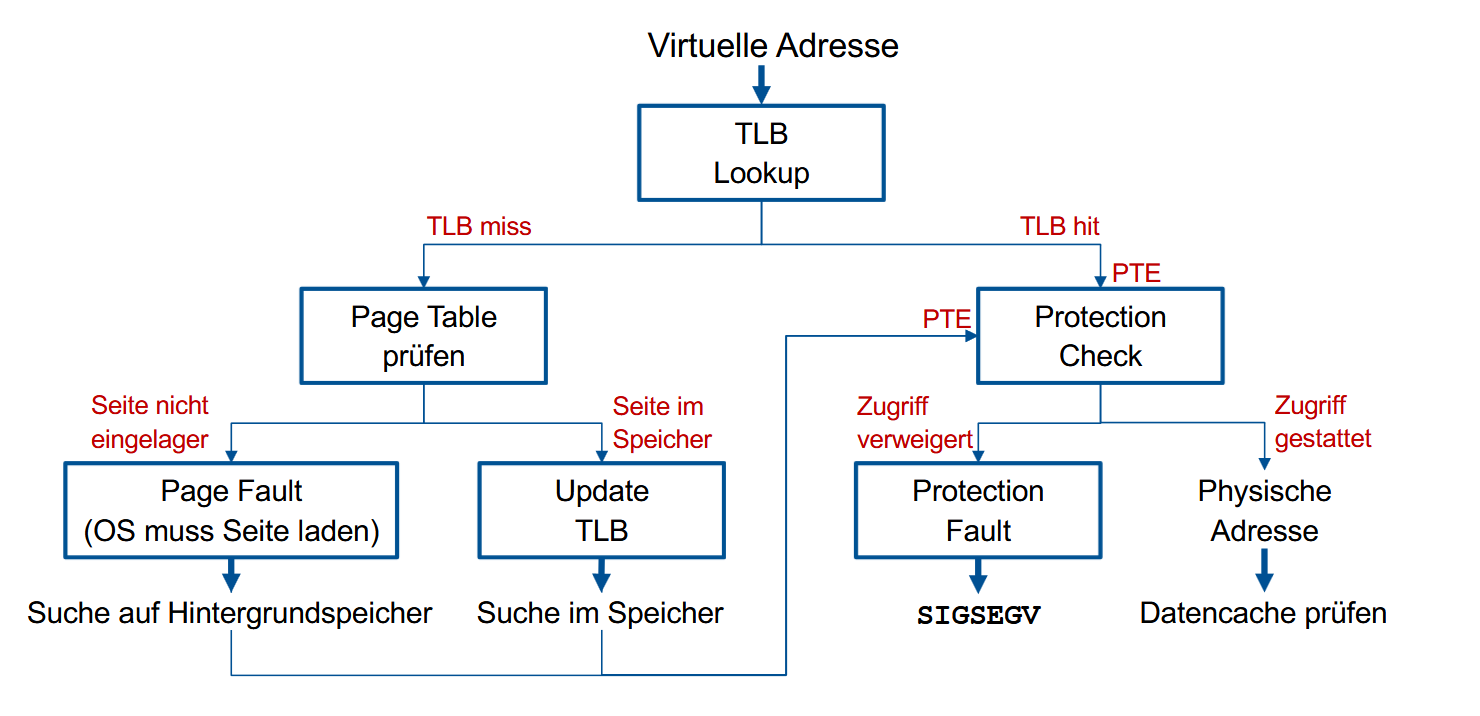
页面置换算法（Seitenersetzungsstrategien）

替换页面的时候，我们有3个问题需要考虑：当内存满了，我们应该

在什么时候加载页面？

针对这个问题我们有2种方法：
1. 按需分页（On-Demand Paging）：页面只有在确实被访问到时，才会被加载到主存。
2. 预取（Prefetching）：会提前加载页面以备不时之需。但这样一来又会回到一开始的问题，我们需要在提前多久加载哪些内容呢？
将页面加载到哪里？

所有页框（Kacheln）地位相同，一般不需要策略决定。但在实际中操作系统一般会对内核代码和内核数据做特殊处理，比如说恒等映射（Identity Mapping），即虚拟地址 = 物理地址。这样效率会高很多。
如果内存已经满了，我们该把现有的哪一页给换下去？

这些正是我们下面会仔细讲的内容。

理论上最完美的算法当然是替换掉那个下一次将被访问时间最晚的页面。操作系统肯定是无法做到预知未来的，不过我们可以尝试往这个方向靠。

FIFO

跟普通的First-in-First-Out一样，先替换掉最早来的。

例子：

缺点：在实际情况里大部分最早来的都是最重要的，所以之后大概率会多次访问，如果被替换下去了会一直触发Page Fault，开销会很大。

所以相比之下较常用的是它的改版：Second-Chance-Algorithmus。

Second-Chance-Algorithmus

在FIFO的基础上，会给每页第二次机会。

页面被访问时会设置R-bit = 1。如果在队伍首则判断R-Bit的值，等于0就会被替换掉（如果M=1需要先执行写入操作然后再替换），等于1的话就给R-Bit的值更新成0然后挪到队伍尾。

图示：

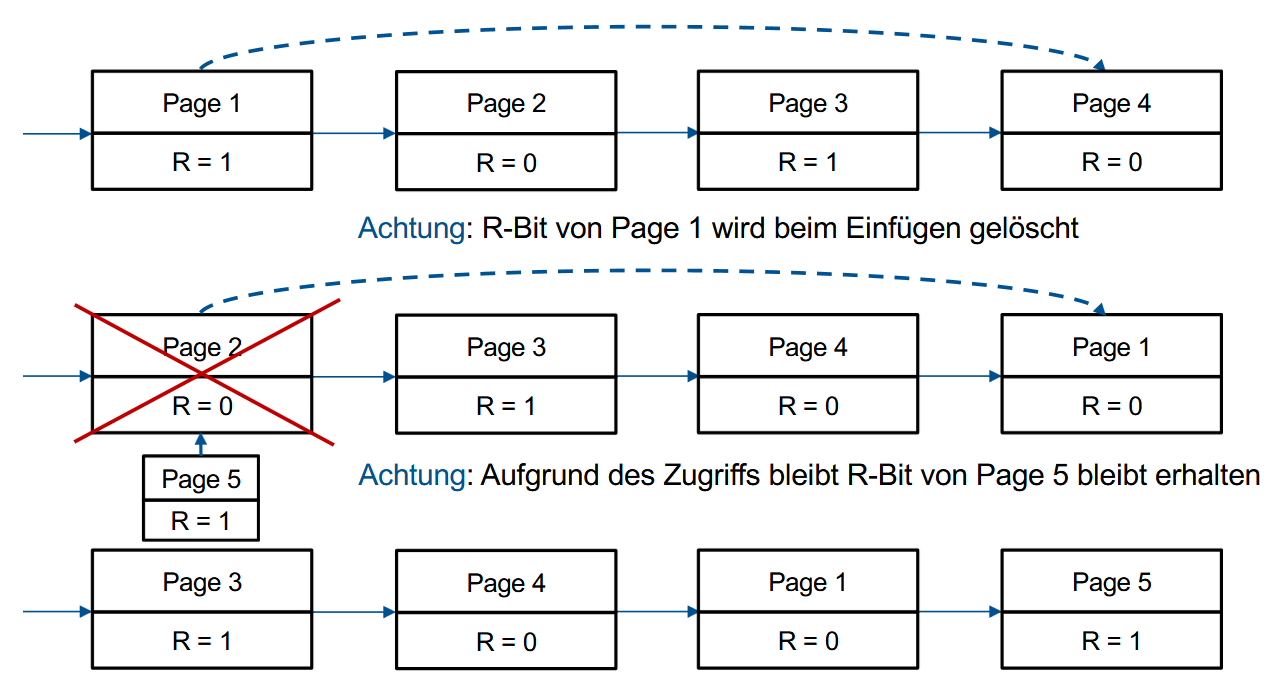
缺点：每次都移动整个队列非常麻烦。

所以使用更高效的数据结构替代队列：Clock。

Clock-Algorithmus

将所有页面按顺序组成一个环状列表（就像Clock一样），有一个“时钟指针”指向其中某个页面，表示当前检查的位置。这个指针用于寻找要替换的页面。

具体流程：

如果当前指向的页面的 R 位为 0：
- 替换这个页面为新页面
- 指针移动一格（顺时针）
如果 R 位为 1：
- 将 R 位清除（设为 0）
- 指针继续移动一格，检查下一个页面
重复 1-2 步骤：
- 直到找到一个 R 位为 0 的页面
- 这个页面会被替换
如果该页面的 M 位（Modified Bit）为 1：
- 将该页面内容写回磁盘
如果 M 位为 0：
- 直接丢弃该页面（因为它未被修改）

具体例子见文章结尾的例题。

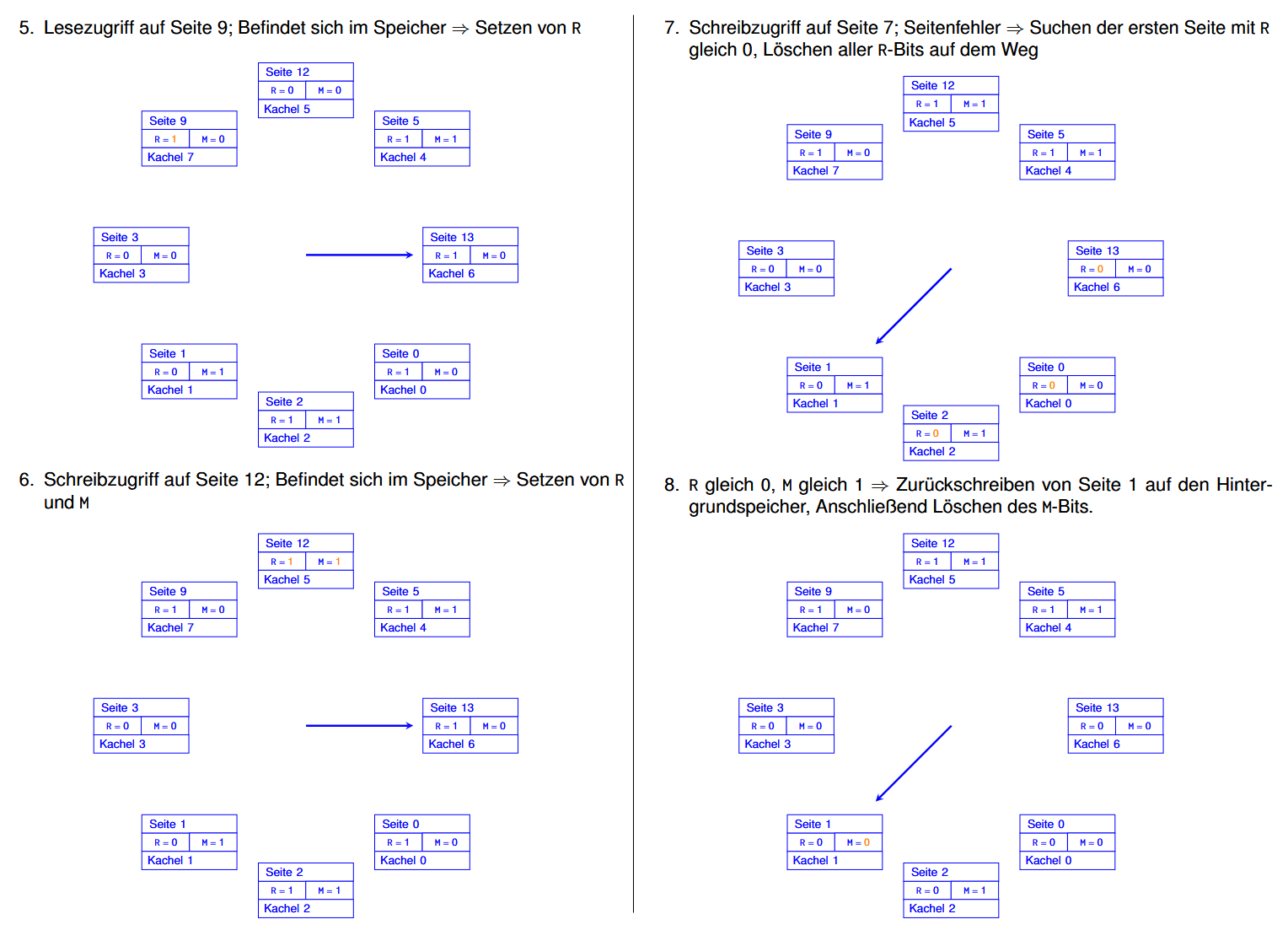
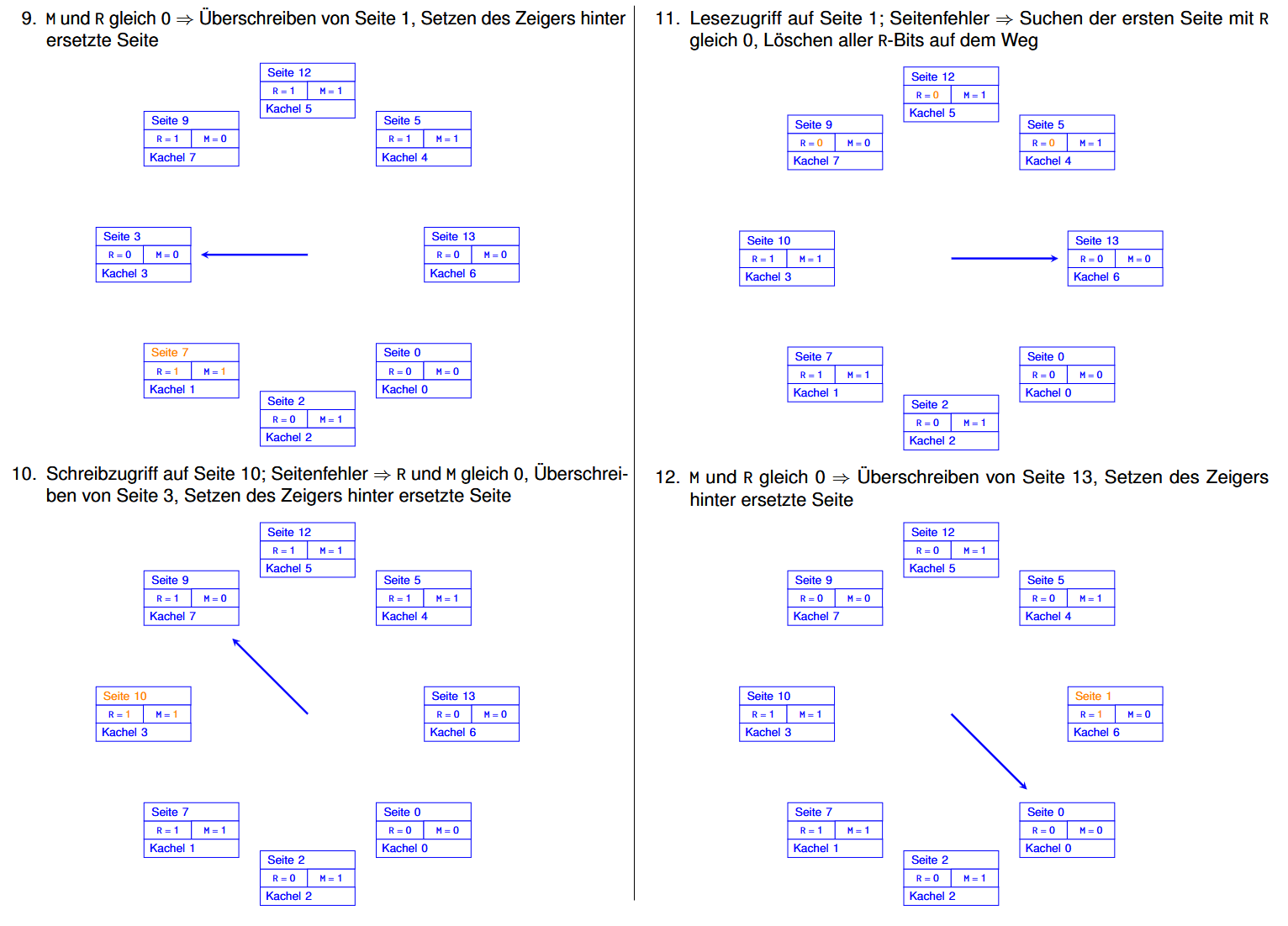
Clock 例子：

假设现在需要进行这些操作：

那么：（每一步里被修改了的内容都用橙色标出来了的）

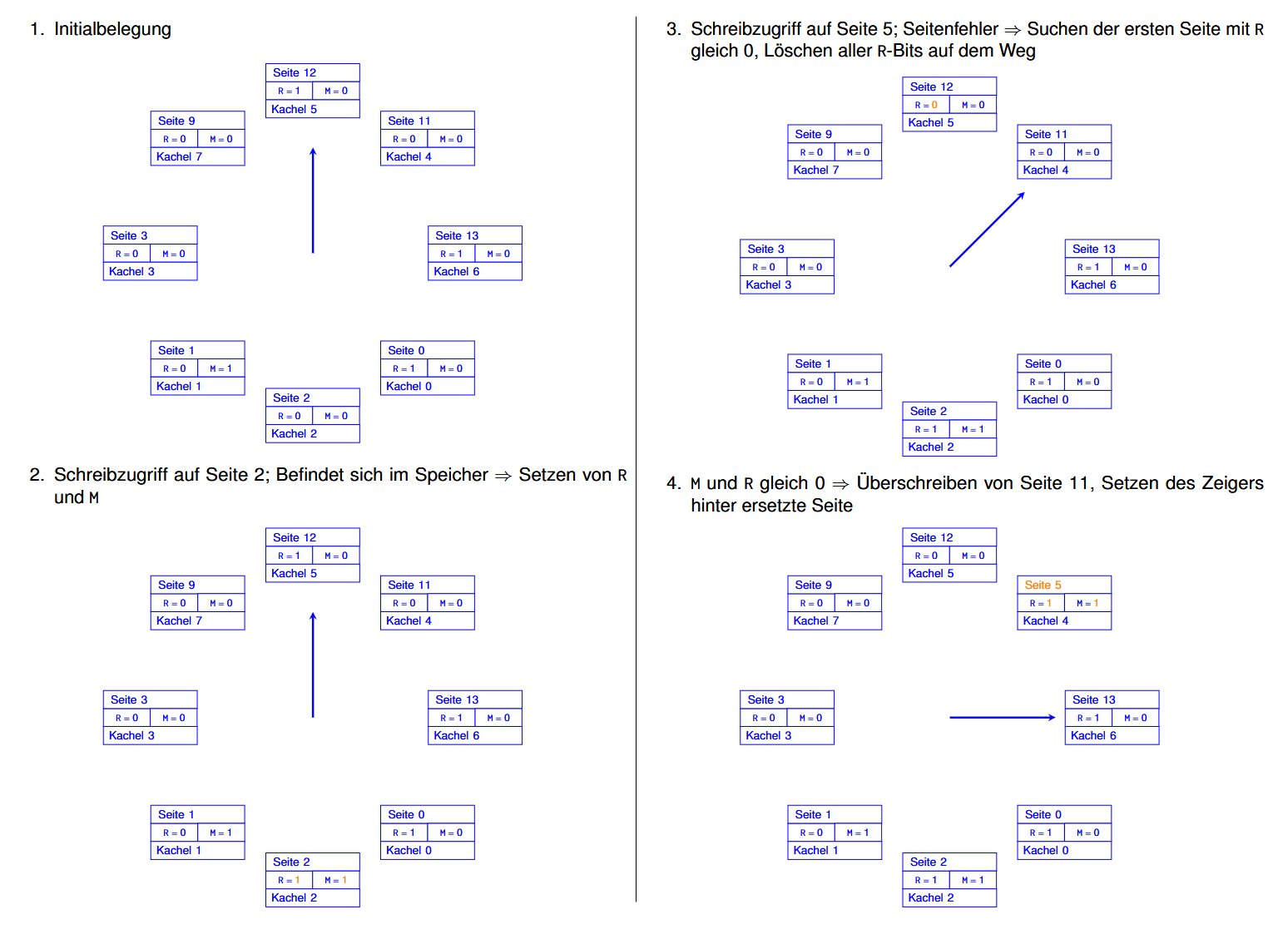
Least Recently Used (LRU)

因为程序的局部性原理（Lokalitätseigenschaft），我们可以假设过去经常使用的页面，未来也可能被再次使用。

当发生Page Fault时，替换掉那个“最长时间没被使用”的页面。

缺点：这个方法的实现需要一个双向链表，记录所有被访问页面，每次访问页面都要把它移到表头（意味着频繁更新），开销太大了，效率不高。

不过我们可以考虑使用软件近似模拟LRU（用“近似但效率更高”的方法来模拟 LRU 的行为趋势）：Not Frequently Used (NFU) 和 Aging。

LRU例子：

假设现在有6页（Page）和4个页框（Kacheln），我们想要按照这个顺序访问：1 3 5 4 2 4 3 2 1 0 5 3 ，那么具体的过程便是：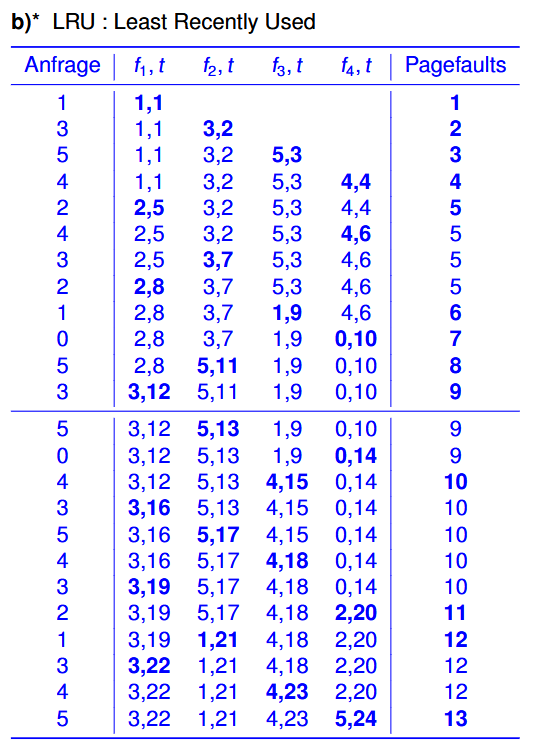

Not Frequently Used (NFU)

给每个页面 P 引入一个软件计数器 $A_p$
- 固定大小，例如 b 位（bit），初始为 0
每次定时器中断（Timer-Interrupt）时：
- 操作系统检查所有页面的 R 位（被访问位）
- 如果某个页面 P 的 R 位被设置：
  - 对应的计数器 $A_p$ 加 1

缺点：NFU并不知道“访问是否是最近的”，只知道总访问次数。比如说一个页面过去访问很多，但最近一直没被访问，NFU仍然会认为它很重要。

为了解决这个问题便需要Aging-Verfahren。

NFU 例子1：

页面编号：0, 1, 2, 3, 4

访问顺序（参考链）：0111221123324434

得到的计数器值：$A_0=1, A_1=5, A_2=4, A_3=3, A_4=3,$

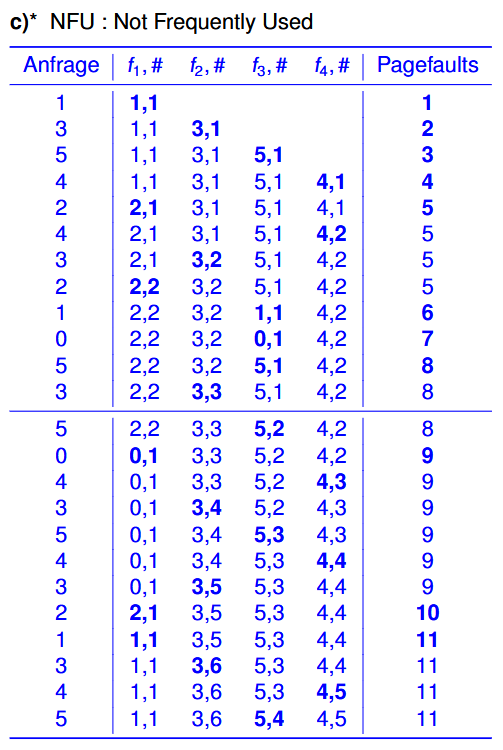
NFU 例子2：

假设现在有6页（Page）和4个页框（Kacheln），我们想要按照这个顺序访问：1 3 5 4 2 4 3 2 1 0 5 3 ，那么具体的过程便是：

Aging-Verfahren

Aging主要的思路是记录访问的“老化”程度（Erfassung der Alterung von Zugriffen）。

首先设置一个固定时间间隔 t（比如 20 毫秒）并记录哪些页面在这个间隔内被访问了。

同样会给每个页面 P 引入一个软件计数器 $A_p$。

每隔 t 的时间都会更新$A_p$：

将计数器向右移一位（shift）
把当前 R 位的值放到最高位

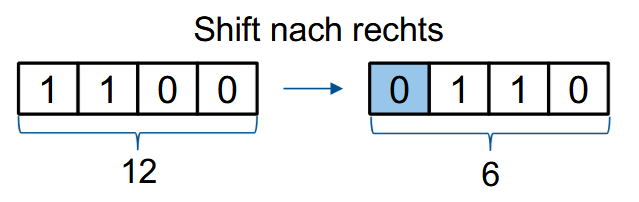
Aging 例子：

假设：Aging 计数器为 4 位（二进制），当前计数器 $A_p = 1100_2 = 12_{10}$，当前的引用位 R = 0。

那么新的 $A_p$ 会变成 $0110_2 = 6_{10}$ 。

当然，Aging也是有一定局限性的，但是我没看懂。（乐）

Working-Set Ersetzungs-Verfahren

前面这些策略全都是基于按需分页（Demand Paging）的，我们现在来看点不一样的。

首先，一个进程当前真正需要的那一批页面（Die Menge der Seiten, die ein Prozess aktuell benötigt）称为：工作集（Working Set）。而抖动（Setitenflattern，Thrashing）指的是当进程频繁地触发Page Fault。

在Working-Set-Modell中：

在任意时刻 t，工作集 w(k, t) 表示进程在最近的 k 次内存访问中访问到的页面集合。（从t往前数k个）

比如说给定一个访问序列：26157777516234123444344，并且将k设置为4，那么w(k, t1) = {3, 4}，w(8, t1) = {2, 3, 4}。

最简单的办法肯定是只替换不在当前工作集内的页面，但是每次都往前追踪k次访问带来的开销太大了。所以我们使用进程的执行时间（Rechenzeit）来近似。

需要先定义几个值：

执行时间区间 $\tau$
时间间隔 I（Clock Tick 间隔）
给每个进程设置一个单调递增的计数器 $Z$，用于近似进程的执行时间（Ausführungszeit /Rechenzeit)，实际使用CPU的时间）
给每一页 P 设置一个计数器 $Z_p$，用于近似上次访问的时间。

Working-Set Ersetzungs-Verfahren：

当发生页面错误时，操作系统会检查所有页的 R 位（R-Bits）：
- 如果R=1 für Seite P：页面属于 Working-Set，不会被替换，但是会将当前的 $Z_p$ 更新成 $Z$ 的值；
- 如果R=0 für Seite P：
  - 如果$Z - Z_P > \tau$：P不属于Working-Set，会被替换掉；
  - 如果$Z - Z_P \leq \tau$：虽然 P 在 I 这段时间里没有被使用过，但还是属于 Working-Set。
如果找到了多个符合条件的候选页：系统会选择 $Z_p$ 最小的那一页，称为 $P_{\text{old}}$。
如果找不到任何页面可以换出（所有页面都还在 Working Set 中）：替换最老的页面（即 $P_{\text{old}}$）。

缺点：实现起来非常复杂。

所以实际中会用 Working-Set Ansatz mit Clock-artiger Verwaltung der Seiten。

Working Set with Clock

malloc()

Linux中的内存管理

使用4级页表（4-stufige Pagetabelle）。

内存分配（Speicher-Allokation）：

Buddy 分配器（Buddy-Allocator，基于之前讲的Buddy-Algorithm）：最小分配单位为页（page）

页面替换策略（Seitenersetzungsstrategie）：

使用 Swap 区：页不会立即被换出，而是暂存在 Swap 区
操作系统会保留一部分空闲帧（Frames），以便快速加载需要的页面
使用 Clock 替换算法的一个变种作为页面替换策略